Neural networks are epicycles

Recently there was a paper that studied what happens when you train neural networks to learn planetary orbits. What it means to “train” a neural network to “learn” some phenomenon is to make it try to find mathematical equations to approximate that phenomenon. The question being probed was whether NNs could learn the underlying physics of the data, that is, Newton’s laws. That’s certainly something that a “super-intelligence” ought to be able to do, right?

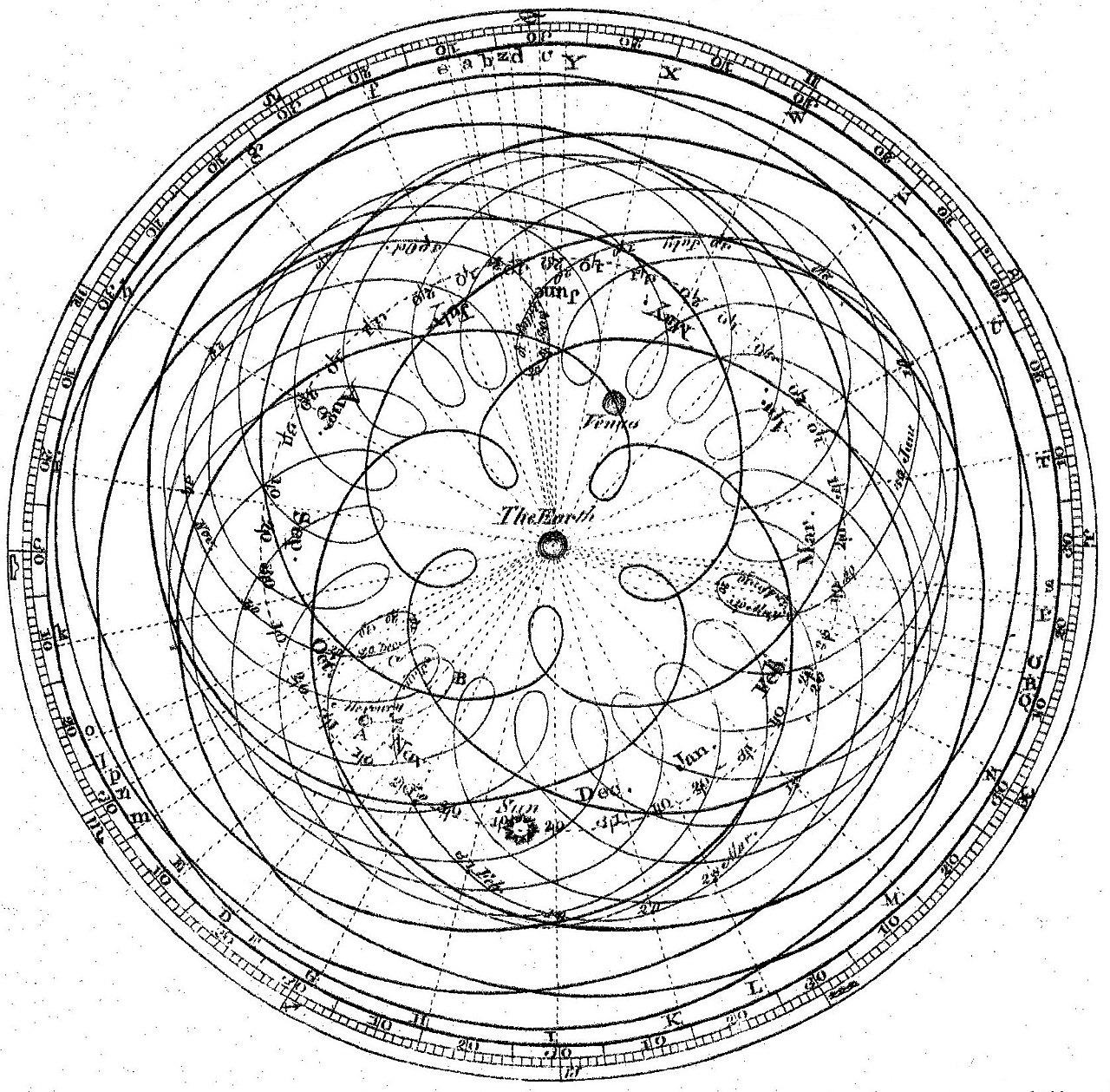
Well, as it turned out, although the model learned the orbits with high empirical accuracy, when they looked into the actual math equations that were derived, they did not resemble Newton’s laws at all. They were a total garbled and inconsistent mess, resembling something like epicycles, the pre-Copernican theory of planetary motion based on circles orbiting circles orbiting circles, rather than the elegance of Newton. So what gives?

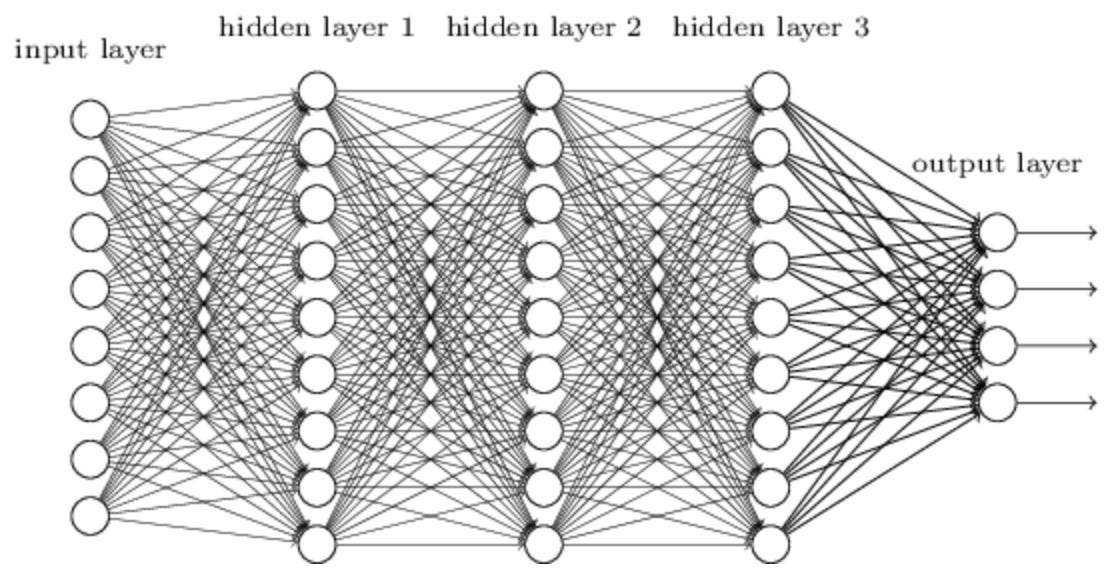
In fact, this result should not be surprising at all; it should have been obvious as soon as the research questions were raised. Neural networks and epicycles are not only analogous, they’re actually different implementations of the same idea: To approximate something, you can do so by building an iterated system where at each step you correct the errors of the previous steps via a simple mathematical mechanism. Neural networks implement this idea via a sequence of layers, each of which consists of simple elements called perceptrons. Each layer corrects the errors of the previous assemblage of layers. The “deep” of “deep learning” refers to the use of a large number of such layers. Epicycles implement this idea via a sequence of circles, each of which corrects the errors of the previous assemblage of circles.

Given such a system, the a priori assumption should not be that it yields simple solutions, but that it yields complex ones. This is almost definitionally true, as the word complex literally means composed of many parts. Neural networks are composed of many layers, and epicycles are composed of many cycles. This is why the result that the neural network learns “laws” more resembling epicycles than Newton should be completely unsurprising.

Expecting a deep neural network to derive Newton’s inverse-square law is like expecting an epicycle model to stumble onto heliocentrism.

---

Now, there is nothing intrinsically wrong about the use of approximation systems; complexity on its own isn’t necessarily better or worse. Such systems are used to great effect all over mathematics and engineering. A canonical example is Fourier series — sums of sines and cosines — which form the backbone of our entire telecommunications infrastructure. Indeed, epicycles can be thought of as an early form of Fourier analysis.

The only problem arises when we think of these approximations as providing metaphysical laws, rather than giving us what exactly we asked for, which is, again, just empirically accurate approximation.

We may denigrate epicycles as pseudoscience today, but in fact they were, and remain, a surprisingly accurate model of planetary motion. In Structure of Scientific Revolutions, Thomas Kuhn argued that the main reason to discard epicycles and geocentrism was not for reasons of empirical accuracy, but rather for human reasons — because Newtonian physics and heliocentrism is a much simpler conceptual theory requiring only a single notion of gravitational force, rather than a complicated notion of orbits around orbits around orbits, requiring correction after correction after correction.

That is to say, the empirical accuracy of a theory may or may not correspond to other desirable properties of the theory, such correctness, simplicity, generalizability to new contexts, or human understandability.

---

The story with LLMs mirrors much of the above discussion although with some subtle differences.

First of all, natural language is different from other domains because it is a universal substrate. Planetary orbit data is just about planetary orbits. But natural language data includes essentially everything. It contains data about planetary orbits, too, in addition to data about every other conceivable topic, such as nuclear power plants, dinosaurs, causal inference, Avril Lavigne, and the history of Ancient Greece.

Neural networks and epicycles try to infer an underlying structure behind the data they are given. When the data is just planetary orbits, they will learn a set of “laws” for the orbits, which is likely to be more complex than necessary, as explained above. But when the data is all the text on the internet, then the “laws” that they derive must be more robust, because these “laws” need to conform with a larger set of phenomena, not just isolated phenomena like planetary motion — or so the argument goes.

Indeed, this argument does seem to hold in many instances! A simple example is grammar. Have you ever seen an LLM make a grammatical error? It happens — but it’s very rare. Grammar is a “latent variable” behind most of the text that the LLM sees during training. This means that grammar influences the text, but it is not explicitly given to the model. Same as the influence of Newton’s laws on planetary motion. The LLM must derive grammar as an underlying “law”. The fact that grammatical errors made by LLMs are so rare, even in novel scenarios, seems to indicate that the LLMs have in fact derived the correct grammatical laws.

But the argument is decidedly not true in other instances, especially for factual information. Hallucinations are epicyclic. For example, when you ask for citations and you get a list of research papers that don’t exist, it’s because the model has imagined a false universe in which those papers do exist. Research papers are factual entities which do not have any particular structure or law that underlies their existence. When they exist, they exist by a combination of random chance and happenstance, as a matter of what happens to be funded and what happens to be discovered by researchers. So in this case, the model tries to find structure where there is none. It derives a theory of epicycles for the existence of research papers, when a better theory would be no theory at all.

---

Where does this leave us in our assessment of LLMs and AI more broadly? Are they truly intelligent, understanding the true metaphysical nature of reality, or are they just epicyclic snake oil?

Sorry to be boring, but there is no straightforward general answer. The model sometimes learns a correct underlying world model, and other times it makes up a nonsensical epicyclic model. There is as yet no real way to control this. There is as yet no real way to predict the correctness of the world model in any given domain.

The main thing we can say about a deep neural network is that it should achieve high empirical accuracy in any domain that is well-represented in its training data. Whether they can go beyond that statement, whether they can usefully generalize, can’t be known in advance. The only way to find out is again empirical, to just try things and observe the results.